DERIVADA DIRECCIONAL.
El concepto general de una derivada aplicado a
funciones multi-variable viene expresado en la Derivada direccional.
Esta representa la tasa de cambio de una función en cualquier dirección dada por un vector.
Para una función de dos variables, la derivada direccional viene definida como:
Esta representa la tasa de cambio de una función en cualquier dirección dada por un vector.
Para una función de dos variables, la derivada direccional viene definida como:
La derivada direccional se puede determinar usando elementos vectoriales.
Para tal caso debemos establecer el vector gradiente así como el vector unitario que nos indica la dirección de cambio.
La expresión para determinar la Derivada direccional es:
Consideremos la función de dos variables:
Su vector gradiente viene expresado como:
La importancia del vector gradiente es que apunta en la dirección de máximo cambio. Asi la Derivada direccional máxima positiva es:
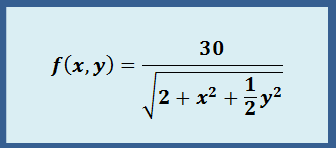
Dijo que serían ejercicios resueltos u.u
ResponderEliminarGracias por los vídeos!
ResponderEliminar